Composite Concave
Linear Programming

Practioners' Court

As we all know only too well, the world out there is not linear! Thus, very often the choice of LP as a modelling and analysis framework involves compromises.

CCLP enables you to partially free yourself from the tyranny of LINEARITY in that it provides you with a methodology for dealing with a large class of highly nonlinear objective functions.

Using CCLP you apply LP in a new way to solve more realistic representation of your real-world nonlinear optimization problems.

Unfortunately, as you know, at present commercial LP software packages do not support this feature. In fact, many do not support simple parametric analysis techniques described in introductory OR textbooks.

Some LP software developers argue that they do not provide these facilities because such facilities were not requested by their users. Well, it is perhaps time for you to do something about it!!!

Using simple parametric analysis techniques of the simplex method CCLP will enable you to solve large scale minimization problems subject to the usual linear constraints but having nonlinear objective functions such as

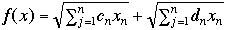
and this

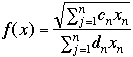
and this

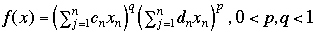
Now, if you have not seen such functions before, it is not because they do not appear in Nature, but more likely because they were difficult to handle. But now that they can be handled by CCLP, there is no reason why they should not be used.

The following example represents a very large and important subcalss of CCLP problems.

Handling soft constaints via CCLP

Suppose that you have a standard LP (minimization problem), except that one of the ingredients in the overall cost involves a resource whose cost is subject to the usual economies of scale structure. Thus, the cost of this resource is of the form:

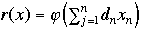
where 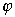is a nondecreasing concave function.

The problem under consideration is then as follows:

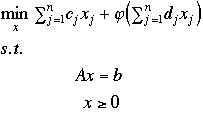
This is a typical CCLP problem par exellence.

If after this visit you'll feel that CCLP can handle some of your nonlinear programming problems, request your LP software developer to add the CCLP capability to its product.

You may also wish to send us a short description of your problem so that we can add it to our Problems Set.

And until your LP software takes care of this matter, do not hesitate to contact us with regard to issues concering the implementation of CCLP techniques using LP software that does not support this feature yet.